排序算法重温

Algorithm

原理

发布日期: 2023-06-08

文章字数: 1.5k

阅读时长: 6 分

时隔两年多的排序算法重温。

快排

原理：快排通过分治的方式实现排序
过程：

将数列划分为两部分（要求保证相对大小关系）。
保证前一个子数列中的数都小于后一个子数列中的数。为了保证平均时间复杂度，一般是随机选择一个数 $m$ 来当做两个子数列的分界。
递归到两个子序列中分别进行快速排序。
维护一前一后两个指针 $p$ 和 $q$，依次考虑当前的数是否放在了应该放的位置（前还是后）。如果当前的数没放对，比如说如果后面的指针 $q$ 遇到了一个比 $m$ 小的数，那么可以交换 $p$ 和 $q$ 位置上的数，再把 $p$ 向后移一位。当前的数的位置全放对后，再移动指针继续处理，直到两个指针相遇。
无需合并，此时数列已经完全有序。

代码实现

def quick_sort(alist, first, last):
    if first >= last:
        return
    mid_value = alist[first]
    low = first
    high = last
    while low < high:
        while low < high and alist[high] >= mid_value:
            high -= 1
        alist[low] = alist[high]
        while low < high and alist[low] < mid_value:
            low += 1
        alist[high] = alist[low]
    alist[low] = mid_value
    quick_sort(alist, first, low - 1)
    quick_sort(alist, low + 1, last)

特点

快速排序是在冒泡排序的基础上改进而来的，冒泡排序每次只能交换相邻的两个元素，而快速排序是跳跃式的交换，交换的距离很大，因此总的比较和交换次数少了很多，速度也快了不少。
稳定性：不稳定（经过排序之后，相同值的元素的相对位置可能发生改变）
时间复杂度：最优时间复杂度和平均时间复杂度为${O(n logn)}$，最坏时间复杂度为${O(n^2)}$
对于最优情况，每一次选择的分界值都是序列的中位数;
对于最坏情况，每一次选择的分界值都是序列的最值。
在实践中，几乎不可能达到最坏情况，而快速排序的内存访问遵循局部性原理，所以多数情况下快速排序的表现大幅优于堆排序等其他复杂度为 O(n \log n) 的排序算法。

空间复杂度：快速排序只是使用数组原本的空间进行排序，所以所占用的空间应该是常量级的，但是由于每次划分之后是递归调用，所以递归调用在运行的过程中会消耗一定的空间，在一般情况下的空间复杂度为 O(logn)，在最差的情况下，若每次只完成了一个元素，那么空间复杂度为 O(n)。所以一般认为快速排序的空间复杂度为 O(logn)。

经典题型实战

剑指 Offer II 076. 数组中的第 k 大的数字
给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

Python 题解

class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        def quicksort(nums, first, last, k):
            mid = nums[first]
            low = first
            hign = last
            while low < hign:
                while low < hign and nums[hign] >= mid:
                    hign -= 1
                nums[low] = nums[hign]
                while low < hign and nums[low] < mid:
                    low += 1
                nums[hign] = nums[low]
            nums[low] = mid
            if low == k:
                return mid
            elif low > k:
                return quicksort(nums, first, low - 1, k)
            else:
                return quicksort(nums, low+1, last, k)
        return quicksort(nums, 0, len(nums)-1, len(nums)-k)

堆排

原理：利用二叉堆这种数据结构而设计的一种排序算法，其本质是建立在堆上的选择排序。
堆：堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。
堆的可视化如下图所示（图源）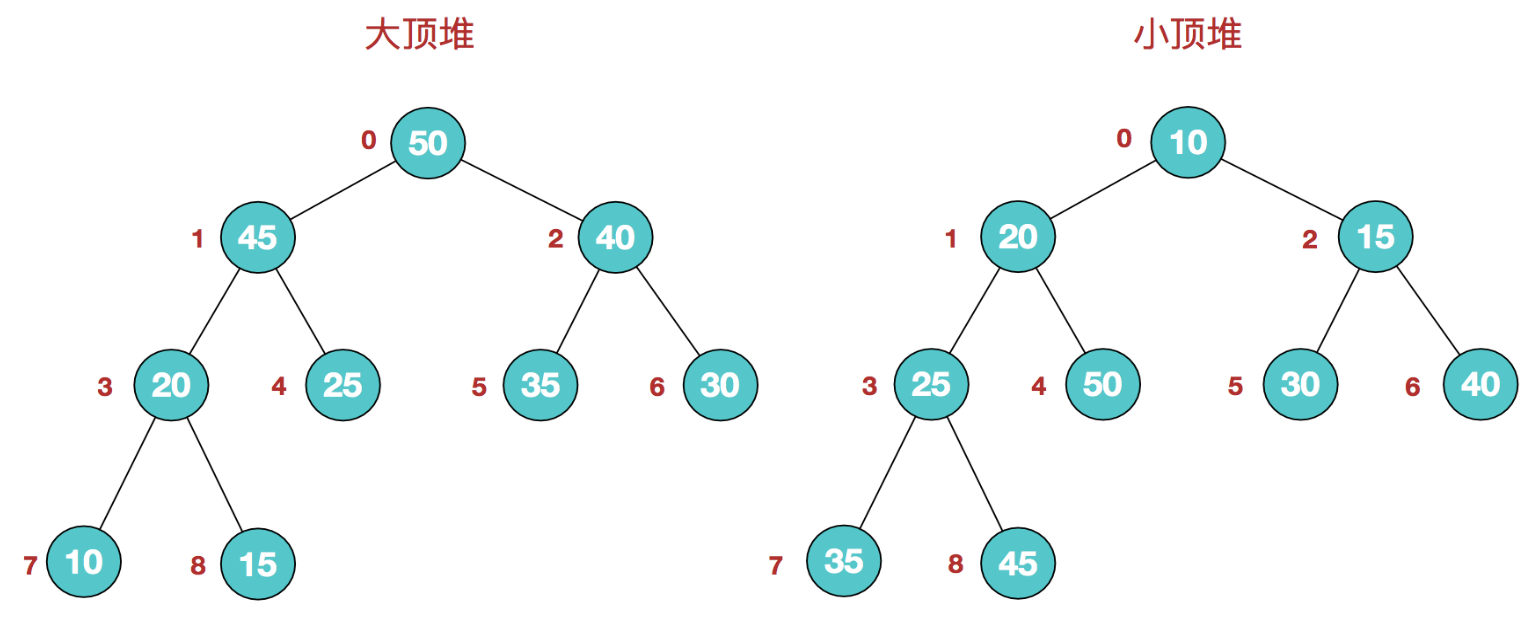

按层编号堆中的节点，这种逻辑结构映射到数组中为（图源）

基本思想：将待排序序列构造成一个大顶堆，取出堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值，维持残余堆的性质。之后将堆顶的元素取出，作为次大值，与数组倒数第二位元素交换，并维持残余堆的性质。以此类推，在第 $n-1$ 次操作后，整个数组就完成了排序。

代码实现

def sift_down(arr, start, end):
    # 计算父结点和子结点的下标
    parent = int(start)
    child = int(parent * 2 + 1)
    while child <= end: # 子结点下标在范围内才做比较
        # 先比较两个子结点大小，选择最大的
        if child + 1 <= end and arr[child] < arr[child + 1]:
            child += 1
        # 如果父结点比子结点大，代表调整完毕，直接跳出函数
        if arr[parent] >= arr[child]:
            return
        else: # 否则交换父子内容，子结点再和孙结点比较
            arr[parent], arr[child] = arr[child], arr[parent]
            parent = child
            child = int(parent * 2 + 1)

def heap_sort(arr, len):
  # 从最后一个节点的父节点开始 sift down 以完成堆化 (heapify)
    i = (len - 1 - 1) / 2
    while(i >= 0):
        sift_down(arr, i, len - 1)
        i -= 1
  # 先将第一个元素和已经排好的元素前一位做交换，再重新调整（刚调整的元素之前的元素），直到排序完毕
    i = len - 1
    while(i > 0):
        arr[0], arr[i] = arr[i], arr[0]
        sift_down(arr, 0, i - 1)
        i -= 1