BEV模型常用LOSS总结,以Pytorch用法为例进行介绍
分类
CrossEntropyLoss 交叉熵
torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=- 100, reduce=None, reduction=’mean’, label_smoothing=0.0)

交叉熵主要用于处理分类任务。当类别不均衡的时候,可以通过给不同的类别添加不同的权重进行平衡。
# Example of target with class indices
loss = nn.CrossEntropyLoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(5)
output = loss(input, target)
output.backward()
# Example of target with class probabilities
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5).softmax(dim=1)
output = loss(input, target)
output.backward()Focal loss
Focal Loss 就是一个解决分类问题中类别不平衡、分类难度差异的一个 loss,它实际上一个基于交叉熵的改进版本。以二分类为例,公式定义如下
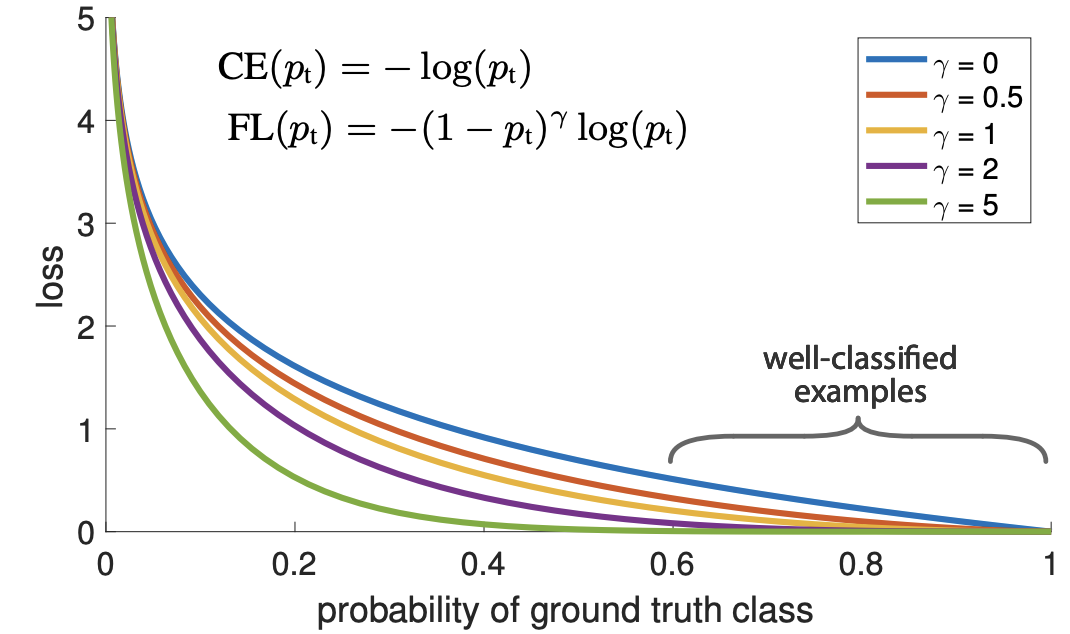
Pytorch实现
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, Dataset
import torchvision
import torchvision.transforms as F
from IPython.display import display
class FocalLoss(nn.Module):
def __init__(self, weight=None, reduction='mean', gamma=0, eps=1e-7):
super(FocalLoss, self).__init__()
self.gamma = gamma
self.eps = eps
self.ce = torch.nn.CrossEntropyLoss(weight=weight, reduction=reduction)
def forward(self, input, target):
logp = self.ce(input, target)
p = torch.exp(-logp)
loss = (1 - p) ** self.gamma * logp
return loss.mean()KLDivLoss KL散度
torch.nn.KLDivLoss(size_average=None, reduce=None, reduction=’mean’, log_target=False)

KL散度的取值范围是$[0, +\infty)$,当两个分布接近相同的时候KL散度取值为0。KL散度和交叉熵之间相差一个常数,这个常数是信息熵。
不对称性。尽管KL散度从直观上是个度量或距离函数,但它并不是一个真正的度量或者距离,因为它不具有对称性,即$D_{KL}(p||q) \ne D_{KL}(q||p)$
>>> import torch.nn.functional as F
>>> kl_loss = nn.KLDivLoss(reduction="batchmean")
>>> # input should be a distribution in the log space
>>> input = F.log_softmax(torch.randn(3, 5, requires_grad=True), dim=1)
>>> # Sample a batch of distributions. Usually this would come from the dataset
>>> target = F.softmax(torch.rand(3, 5), dim=1)
>>> output = kl_loss(input, target)
>>> kl_loss = nn.KLDivLoss(reduction="batchmean", log_target=True)
>>> log_target = F.log_softmax(torch.rand(3, 5), dim=1)
>>> output = kl_loss(input, log_target)回归
L1 loss (MAE loss)
torch.nn.L1Loss(size_average=None, reduce=None, reduction=’mean’)

>>> loss = nn.L1Loss()
>>> input = torch.randn(3, 5, requires_grad=True)
>>> target = torch.randn(3, 5)
>>> output = loss(input, target)
>>> output.backward()L2 loss (MSE loss)
torch.nn.MSELoss(size_average=None, reduce=None, reduction=’mean’)

>>> loss = nn.MSELoss()
>>> input = torch.randn(3, 5, requires_grad=True)
>>> target = torch.randn(3, 5)
>>> output = loss(input, target)
>>> output.backward()Smooth L1 loss
torch.nn.SmoothL1Loss(size_average=None, reduce=None, reduction=’mean’, beta=1.0)

优点:Smooth L1 loss主要是在预测结果和ground-truth相差大时起到限制梯度的作用。在$x$较小时,对$x$的梯度也会变小,而在$x$很大时,对$x$的梯度的绝对值达到上限 1,也不会太大以至于破坏网络参数。完美地避开了$L_1$和$L_2$损失的缺陷,不会导致梯度爆炸。其函数图像如下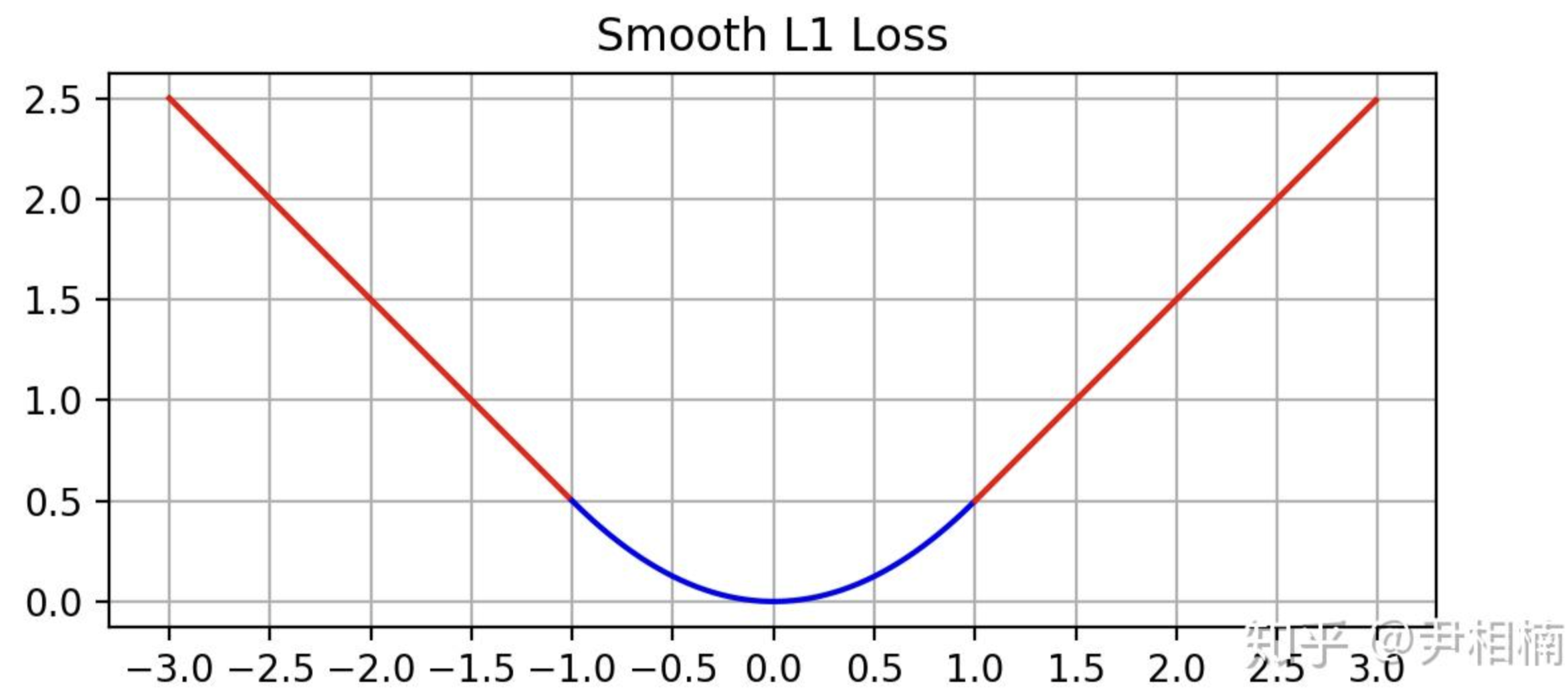
曼哈顿距离
曼哈顿距离实际上就是两个点在标准坐标系上的绝对轴距总和。
GIoU loss (Generalized Intersection over Union)
GIoU loss即泛化的IoU损失。当预测框与真实框之间没有任何重叠时,两个边框的交集(分子)为0,此时IoU损失为0,因此IoU无法算出两者之间的距离(重叠度)。另一方面,由于IoU损失为零,意味着梯度无法有效地反向传播和更新,即出现梯度消失的现象,致使网络无法给出一个优化的方向。
参考
https://pytorch.org/docs/
https://www.zhihu.com/question/58200555/answer/621174180
https://zhuanlan.zhihu.com/p/552132010

