自动驾驶常见坐标转换与Nuscenes中的坐标转换实战
自动驾驶常见坐标转换
自动驾驶系统涉及很多传感器,每个传感器处于不同的坐标系统,要统一处理来自不同传感器的数据,就涉及到传感器之间的坐标转换。以下将主要围绕视觉系统涉及到的坐标转换进行展开。
相机相关的基础知识
光轴:一条垂直穿过理想透镜中心的光线。
焦点:与光轴平行的光线射入凸透镜时,理想的凸镜应该是所有的光线会聚在透镜后面一点上,这个会聚所有光线的一点,就叫做焦点。
焦距:一般指镜片的中心到焦点为止的光轴上的距离,入射平行光线(或其延长线)与出射会聚光线(或其延长线)相交,就能确定折射主面,这个想象的平面与镜头光轴相交处就是主点。
光圈:光圈对照片的影响主要有两大项,一是镜头的进光量,二是相片的景深。光圈越大(f 值越小),景深越浅(前景/背景看上去就像化掉一样);光圈越小(f 值越大),景深越深(前景/背景看上去比较清楚)
相机坐标系统
为了清晰描述整个相机坐标系统,首先需要明确将要涉及到的坐标系的定义
- 像素坐标系
像素坐标系是二维坐标系,它用于描述像素点在图像中的位置。像素坐标系一般以左上角为原点,向右为u轴正方向,向下为v轴正方向,用$(u, v)$表示其坐标值。 - 图像坐标系
以光心在图像平面投影为原点的坐标系 ,X轴和Y轴分别平行于图像平面的两条垂直边,用$(x, y)$表示其坐标值。图像坐标系是用物理单位表示像素在图像中的位置。 - 相机坐标系
相机坐标系是一个三维空间坐标系,以相机光心为原点的坐标系。X轴和Y轴分别平行于图像坐标系的X轴和Y轴,相机的光轴为Z轴,z轴垂直于像平面且朝向像平面,Z轴和像平面的交点正是图像坐标系的像主点。用$(x_c, y_c, z_c)$表示其坐标值。 - 世界坐标系
世界坐标系是一个三维直角坐标系,它是一个绝对坐标系,旨在将空间中的所有点都统一到同一个坐标系下表达。在不同的应用场景中,世界坐标系的定义并不一样,可以根据实际情况自由确定。在自动驾驶场景中,常将各传感器数据统一到LiDar坐标系或者IMU坐标系下。用$(x_w, y_w, z_w)$表示其坐标值。
相机->像素(相机内参)
相机将三维世界中的坐标点映射到二维图像平面的过程可以用几何模型进行描述,其中比较经典又简单有效的是针孔模型。针孔模型描述了一束光线通过针孔之后,在针孔背面投影成像的关系。由于镜头上存在透镜,光线投影到成像平面的过程中会产生畸变,将在相机畸变这篇文章中具体介绍。针孔成像模型如下图所示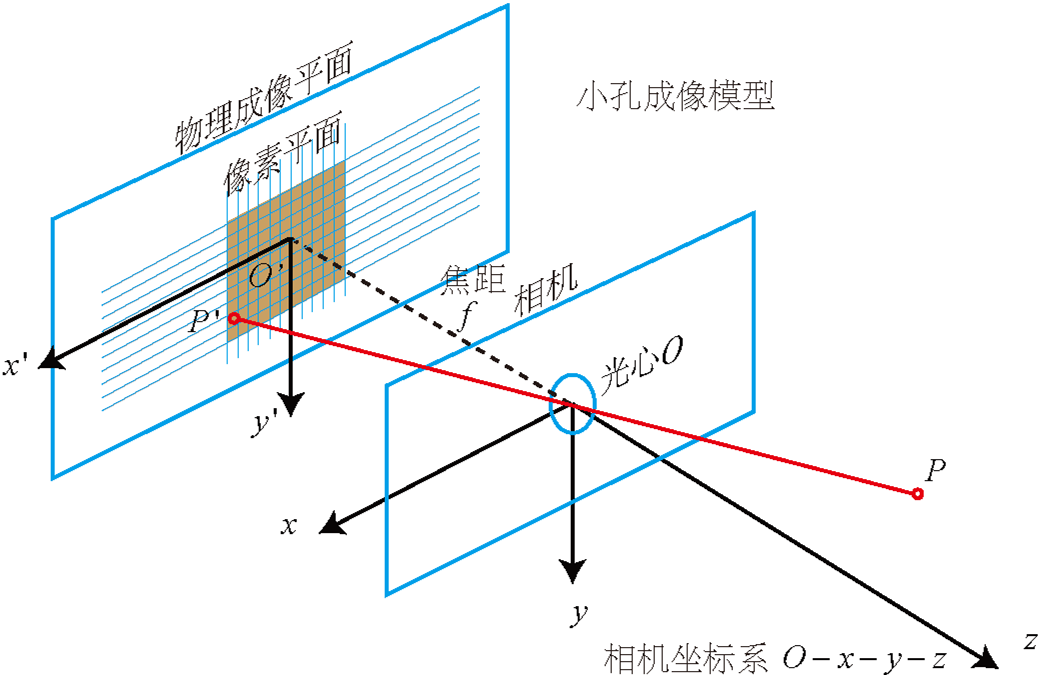
设${O-x-y-z}$为相机坐标系,$O$为相机的光心。空间中一点$P$经过小孔$O$投影后落在物理成像平面${O’-x’-y’}$上,成像点为$P’$。设$P$的坐标为$[X, Y, Z]^T$,$P’$为$[X’, Y’, Z’]^T$。设物理成像平面到小孔的距离为$f$(焦距)。根据三角形相似关系,
负号表示成的是倒立的像,但是实际成像并不是倒像。将成像平面对称地放到相机前面,和三维空间点一起放在相机坐标系的同一侧,上式中的负号就可以去掉。
把$X’$、$Y’$放在等式左侧,整理得到
由此,我们得到了点$P$和它的像之间的空间关系,目前所有的单位都可理解成米。由于最终获得的是一个个的像素,还需要在成像平面上对像进行采样和量化。为了描述传感器将感受到的光线转换成像素图像的过程,设在物理成像平面上固定着一个像素平面${O-u-v}$。在像素平面上得到了$P’$的像素坐标$[u, v]^T$。
我们在上文中已经明确了像素坐标系的定义,像素坐标系与成像平面之间,相差了一个缩放和一个原点的平移。设像素坐标在$u$轴上缩放了$\alpha$倍, 在$v$轴上缩放了$\beta$倍。同时,原点平移了$[c_x, c_y]^T$。那么,$P’$的坐标与像素坐标$[u, v]^T$的关系为
合并$\alpha f$为$f_x$,$\beta f$为$f_y$,可得
其中,$f$的单位为米,$\alpha$,$\beta$的单位为像素/米,因此$f_x$,$f_y$,$c_x$,$c_y$的单位为像素。将上式写成矩阵形式为
将$Z$移到左边,可以得到
矩阵$K$通常称为相机内参(Camera Intrinsics)。通常认为相机内参在出厂之后是固定的。也可以通过相机标定自行确定相机内参。
世界->相机(相机外参)
上式中,我们使用的是$P$在相机坐标系下的坐标,由于相机实际上是运动的,$P$的相机坐标应该是它的世界坐标$P_w$根据相机的当前位置变换到相机坐标系下的结果。相机的位姿由其旋转矩阵$R$和平移向量$t$描述,因此有
上式描述的是$P$的世界坐标到像素坐标的投影关系。其中,相机的位姿成为相机的外参(Camera Extrinsics)。外参会随着相机的运动而发生变化。
需要注意的是,点的深度在投影过程中会丢失,这也是多目3D感知中的难点所在。
三维空间刚体运动
上文中,我们使用内外参实现了相机系统相关的坐标转换。在实际使用中,描述刚体在三维空间中的运动可以使用多种方式。这一部分,将对相应知识点进行补充讲解。
坐标系间的欧式变换
两个坐标系之间的运动由一个旋转加上一个平移组成,这种运动称为刚体运动。两个坐标系之间的转换通过欧式变换进行描述。欧式变换由旋转和平移组成。
首先考虑旋转,设某个单位正交基$(e_1, e_2, e_3)$经过一次旋转变成了$(e_1’, e_2’, e_3’)$。对于同一个向量$a$,它在两个坐标系下的坐标为$[a_1, a_2, a_3]^T$和$[a_1’, a_2’, a_3’]^T$。因为向量本身并没有改变,根据坐标的定义有
为了描述两个坐标之间的关系,对上述等式的左右两边同时左乘
等式左边的系数就变成了单位矩阵,所以
将中间的矩阵定义为旋转矩阵$R$,该矩阵由两组基之间的内积组成,描述的是旋转前后同一个向量的坐标转换关系。由于基的长度为1,实际上是各基向量夹角的余弦值,因此该矩阵也称为方向余弦矩阵。
旋转矩阵
旋转向量和欧拉角
四元数
Nuscenes中的坐标转换
nuScenes的传感器坐标系设置如图所示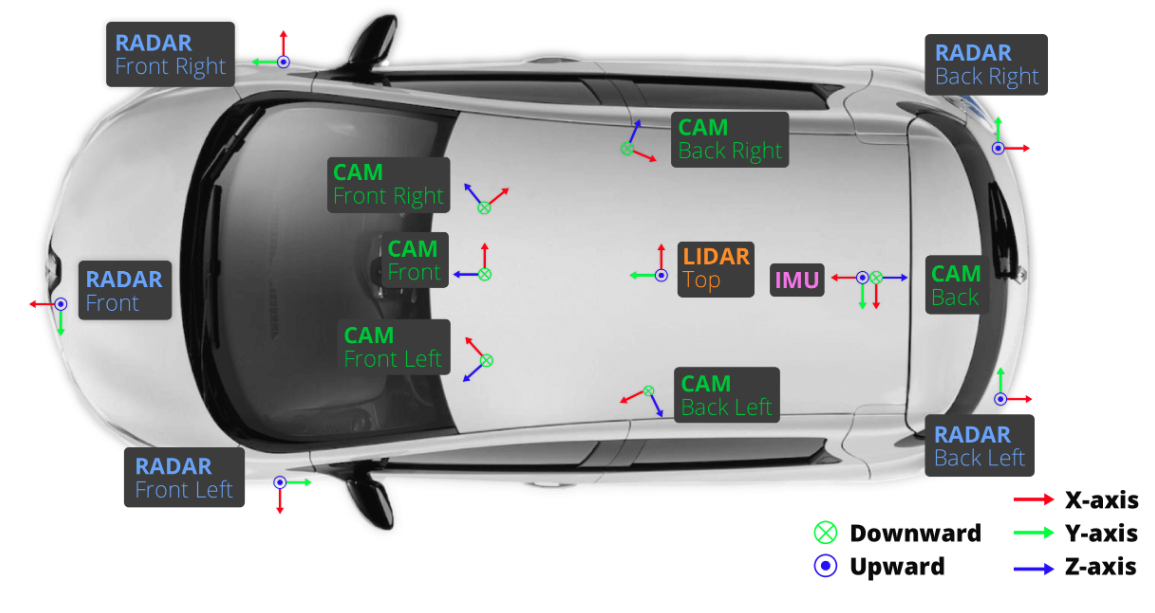
由于在nuScenes数据集中,相机的外参是LiDar到相机的转换矩阵,因此基于nuScenes的BEV研究,通常将LiDar坐标系的XY轴定义为BEV坐标系的XY轴。
图像->LiDar
根据上文,此处主要涉及像素-图像、图像-相机、相机-LiDar共三个步骤。
LiDar->惯导
参考
https://www.nuscenes.org/nuscenes
《视觉SLAM十四讲》—高翔
https://zhuanlan.zhihu.com/p/340751743
https://zhuanlan.zhihu.com/p/374269239
https://zhuanlan.zhihu.com/p/453081175

